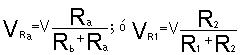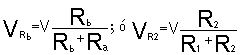Para una mejor descripción vamos a considerar una instalación eléctrica, así pues, cuando ésta se pone en funcionamiento podemos decir que está constituida al menos por un circuito cerrado, por el cual circula una corriente que le permite su funcionamiento. Partiendo de este enunciado como luego se verá, los circuito pueden estar formados por distintas ramas que por su formación se dividen en circuitos serie, circuitos paralelo y a su vez pueden estar formados por la combinación de ambos tipos combinados entre sí.
Todos los circuitos se rigen por unas reglas naturales a las que los hombre les hemos dado el rango de leyes. Estas leyes se basan en la llamada Ley de Ohm que es quien la descubrió, de esta Ley se derivan todas las demás y estas leyes son las que, nos permiten conocer anticipadamente los resultados que se prevén dándolos por buenos, en otros casos se encargan de evitarnos largos procesos que no llevarían a ninguna parte, ya que con el calculo desarrollado nos dicen la inviabilidad del proyecto. Y sin más dilación, vamos a ocuparnos de los siguientes temas:
La Ley de Ohm
George Simon Ohm, descubrió en 1827 que la corriente en un circuito de corriente continua varía directamente proporcional con la diferencia de potencial, e inversamente proporcional con la resistencia del circuito. La ley de Ohm, establece que la corriente eléctrica (I) en un conductor o circuito, es igual a la diferencia de potencial (V) sobre el conductor (o circuito), dividido por la resistencia (R) que opone al paso, él mismo. La ley de Ohm se aplica a la totalidad de un circuito o a una parte o conductor del mismo.
I = V / R ;
V = I x R
Veamos un Ejemplo:
Sabemos que un diodo LED enciende con dos pilas AA o AAA en serie pero (1.7 a 3.2V). Para otras tensiones, es necesario utilizar una resistencia limitadora en serie para evitar que la excesiva corriente lo queme.
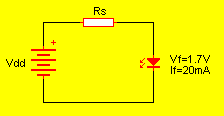
En realidad la fórmula a aplicar no es otra cosa que la tradicional ley de ohms aplicada a un circuito en serie:
RS = (Vdd – Vf) / If
Donde Rs es el valor de la resistencia, Vdd es la tensión de alimentación, Vf es la tensión final requerida por el LED y If es la corriente del mismo. Al restar (Vdd – Vf), obtengo la diferencia de potencial.
Veamos un ejemplo para colocar un LED en el auto…
RS = (12v – 1.7v) / 20mA = 10.3v / 20mA = 515 ohms
Es conveniente siempre ir al valor estándar superior de resistencia para mayor seguridad, en este caso podría ser 590 ohms o bien 680 ohms.
En los circuitos de corriente continua, puede resolverse la relación entre la corriente, voltaje, resistencia y potencia con la ayuda de un gráfico de sectores, este diagrama ha sido uno de los más socorridos:
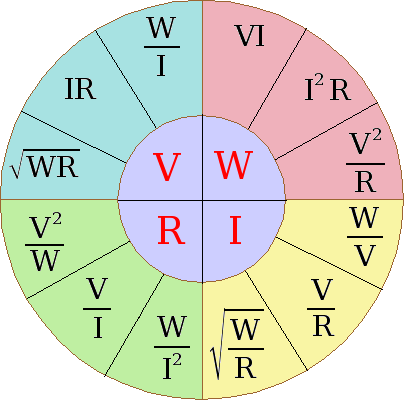
En este grafico puede apreciarse que hay cuatro cuadrantes que representan: V Voltaje, I Corriente, R Resistencia y W Potencia. De modo que, conociendo la cantidad de dos cualesquiera, nos permite encontrar el otro valor. Por ejemplo, si se tiene una resistencia de 1k y en sus extremos se mide una tensión de 10 Voltios, entonces la corriente que fluye a través de la resistencia será V/R = 0’01A o 10mA.
De forma similar, la potencia absorbida por esta resistencia será el cociente de V2 / R = 0’1W o 100mW, otra forma de hallar la potencia es con el producto de V x I o sea, 10V x 0’01 = 0’1W, con esto se confirma lo dicho.
Polaridad de una tensión
Dependiendo del flujo de la corriente en un circuito, una tensión tendrá una polaridad. Se establece que, el polo positivo en un circuito es el que corresponde al punto del que fluye la corriente del generador. La dirección de la corriente se indica con una flecha, como se muestra a continuación:
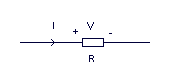
Así, el lado de la resistencia dónde los flujos entran en la resistencia será el polo positivo del voltaje, el polo negativo es donde los flujos salen hacia fuera. Si la resistencia es de 5 W y la corriente es de 2 amperios, entonces el voltaje o la diferencia de potencial sería 10 voltios (V=I x R).
En electrónica, es normal hablar sobre la diferencia de potencial (d.d.p.) con referencia a un punto que normalmente es cero. Si este punto no fuera cero, entonces su valor se indicaría claramente, pero por conveniencia, la mayoría de los sistemas tienen una tierra común o masa que normalmente son cero voltios.
Los circuitos serie
La corriente en un circuito serie es absolutamente la misma en todos sus puntos. Esto es fácil deducirlo al aplicar el principio de que la resistencia total de un circuito es la suma de todas y cada una de las resistencias que lo forman, dicho de otra forma, en el circuito que se muestra a continuación la corriente que lo atraviesa es de 2 mA, para su comprobación partimos de sumar las tres resistencias que lo forman, 2kW + 4kW + 6kW =12kW si la tensión que aplicamos es de 24V, al aplicar la formula, encontramos que la intensidad es de 0’002 A o sea, 2mA. Para el cálculo de la resistencia total en un circuito serie se utiliza esta formula general: RT= R1 + R2 + R3 … .
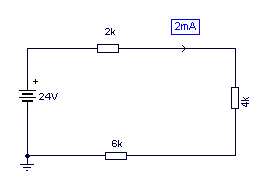
En este caso no hemos considerado la resistencia interna Ri de la fuente de corriente por ser muy pequeña, así como el decremento de la resistencia en las resistencias con el calor provocado por el paso de la corriente, sin embargo si esta Ri por cualquier circunstancia fuera más considerable, esto podría manifestarse con un bajo rendimiento del circuito. Veremos un caso concreto.
En el caso de una batería la cual presenta 12V al medir sus terminales y en cambio al conectar al circuito la carga de una lámpara de coche (12V 100mA), no funciona y sin embargo no está fundida, al medir la corriente de consumo observamos que es de tan sólo 0’05 A. Qué está ocurriendo. Un técnico sospecharía de la carga de la batería y estando la lámpara conectada pasaría a medir la tensión de la batería, obteniendo una lectura de 6V con un consumo de 0’05A.
Dado que la lámpara no se enciende su filamento no se calienta y consecuentemente su resistencia no varía (caso ideal), en estas condiciones el cociente de la tensión de 6V por la corriente de 0’05A nos indica que la resistencia de la lámpara es de 120W, lo esperado.
Otro ejemplo de ayuda con los cálculos. Dos lámparas que indican, 220V – 60W y 220V – 40W respectivamente se encuentran conectadas en serie a una línea de 220V. Qué potencia se transforma en cada lámpara. Ver figura 04.
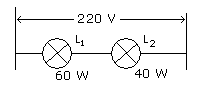
Estos son los cálculos:
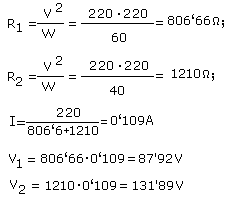
Las pequeñas variaciones son debidas a las fracciones decimales despreciadas.
Circuitos paralelos.
Los circuitos paralelos se caracterizan por estar formados por dispositivos cuyas respectivas resistencias están en paralelo respecto a la tensión de alimentación. La particularidad de un elemento que está en paralelo con otro es que la tensión en ambos es la misma, en cambio la corriente total del circuito es la suma de la corriente que atraviesa cada carga. Para calcular la resistencia total un circuito paralelo, la formula que utilizaremos es la que sigue:
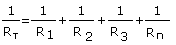
De esta formula como regla general se desprende que, la resistencia total que ofrecen distintas cargas resistivas en un circuito paralelo, es siempre menor que la resistencia de menor valor. La forma del circuito paralelo se aprecia en la figura 06, donde las resistencias pueden representar las cargas de distintos elementos, aplicando la regla general comentada a la figura 06, la resistencia total será: 1’0909 kW.
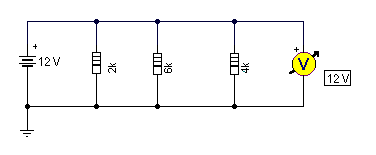
Un nuevo ejemplo puede aclarar más el tema. Entre los puntos A y B del circuito siguiente se aplica una tensión de 12 V. Qué intensidad circulará por el circuito, cual es la intensidad en cada resistencia y de qué potencia debe ser cada resistencia.
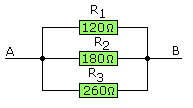
El calculo nos indica que la resistencia total es de 56’38W y de este resultado obtendremos la solución del resto. Así que, la intensidad que atraviesa R1 será el cociente de la tensión por la resistencia que será 0’1A, en R2 será de 0’066A y en R3 será de 0’046A, por lo tanto la corriente en el punto A o en el B será la suma de estos, es decir 0’212A o sea 212 mA.
Hallar el consumo total, es fácil aplicando la formula adecuada. Si aplicamos PT = I2 * R = 2’55W y si aplicamos PT = V * I = 2’54W como vemos en la práctica es el mismo resultado. La potencia de R1 es de 1’2W, la de R2 es de 0’792W y la de R3 es de 0’552W, al sumar estas potencias encontramos la coincidencia con la potencia total de 2’544W.
Circuitos mixtos.
Estos circuitos son combinaciones del tipo serie y paralelo, su resolución resulta ser un poco más laboriosa, sin embargo, el nivel de dificultad sigue siendo el mismo. Para comprender mejor la dinámica a seguir pondremos un ejemplo que nos ayude a comprenderlo mejor.
La propuesta es, con los datos presentados en la figura 08, queremos conocer el valor de R1, la tensión E del Generador, la corriente total IT que suministra al circuito y la PT.
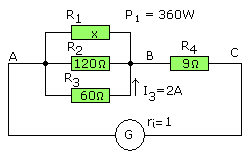
Cálculos:
Como siempre ayudándonos del gráfico del principio, vamos a dar solución al problema planteado. Primero la tensión entre A-B será el producto entre R3 y la corriente que la atraviesa 2A que, nos da 120V. VA-B = 120V.
La intensidad en R2, ahora es fácil de hallar, es el cociente de la tensión A-B y su resistencia, esto es 1A. En cuanto a la corriente que fluye por R1 es, también el cociente del cuadrado de la tensión A-B y la potencia en R1= 360W, esto nos da para R1 = 40W .
De aquí obtenemos la intensidad que la atraviesa, esto nos indica que la intensidad en R1 es de 3A. Así podemos saber que, la corriente total del circuito es de 6A que atraviesa a R4 y la tensión en sus extremos (B-C) será de 54V. La potencia total se obtiene del producto de: PT =174 * 6 =1044W
La tensión del generador G, sabiendo que su resistencia interna es 1 W , la tensión en G es, V= 6 * 1 = 6V, que sumados a los 174 nos da 180V, en el interior de G la tensión es 180 pero G tiene una resistencia interior de 1 W así al exterior sólo presenta los 174V.
Resistencia de absorción.
Cuando necesitamos conectar un equipo a un generador o fuente de tensión, cuya tensión es mayor de la que exige el circuito, podemos poner una resistencia en serie que reduzca la tensión de diferencia. Esta resistencia toma el nombre de resistencia de absorción, su cálculo se lleva a cabo con esta formula:
| Vd – Vu Ra = ————- I |
Vu = Tensión útil
I = Corriente necesaria
El shunt.
Es el acoplamiento de una resistencia a un galvanómetro, si llamamos Rs a la resistencia del shunt y Rg a la del galvanómetro, así como Is e Ig a las intensidades del shunt y del galvanómetro respectivamente, entonces evidentemente la intensidad total IT será:
I = Is + Ig ; y también
Is * Rs = Ig * Rg
En electricidad y electrónica es bastante corriente utilizar un ‘shunt’ que consiste en una resistencia derivada que se agrega a un dispositivo de medida para que la intensidad de la corriente que lo atraviesa sea menor que la intensidad de línea. Sea rg la resistencia interna del galvanómetro, en general y rs la del shunt, ver figura 09.

Por definición se le denomina poder multiplicador m, a la relación entre la intensidad de línea I y la intensidad ig de G y es la constante por la que hay que multiplicar ig para obtener la intensidad de línea I.
| I m = ——- ; ig | [1] |
| I = ig + ix |
que dividiendo por ig;
| ix m = 1+ ——- ig | [2] |
y teniendo en cuenta que la caída de tensión en ambas ramas es idéntica; rg + ig = rs + ix
que igualando con la expresión [2],
| rg ix —– = —– = m -1 rs ig | [3] | |
rg rs =——– m – 1 | [4] |
Esta última es la expresión de la resistencia del shunt en función de la resistencia del galvanómetro y del poder multiplicador.
Así, en muchas ocasiones conviene utilizar un miliamperímetro o un voltímetro para medir magnitudes eléctricas que requieren una escala más alta que la que ofrece el instrumento. Para esto es necesario, como se ha dicho, añadirle una resistencia. Al cociente del valor máximo de la nueva escala dividido por el valor máximo de la escala primaria, es lo que se llama factor de multiplicación como se obtiene en la formula [2].

La cual podemos recordar mejor con esta nueva formula [2a].
Resistencia de compensación.
En muchas ocasiones, ocurre que en medidas eléctricas hay que ‘shuntar’ un miliamperímetro sin que varíe la resistencia intercalada en el circuito, evitando de este modo que se falsee la lectura, para ello, se coloca en serie con el galvanómetro y el shunt una resistencia Rx (resistencia de compensación), tal que el nuevo conjunto presente una resistencia rg idéntica a la que presentaba el galvanómetro sólo.

rg * rs
——— + RX = rg
rg + rs
de donde;
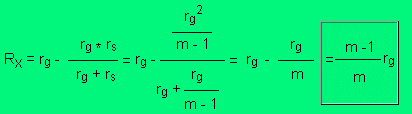
Shunt universal.
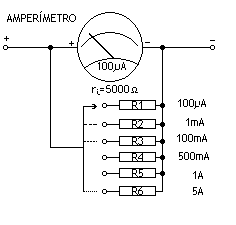
El shunt universal tiene la ventaja de presentar varios multiplicadores en el mismo medidor, pudiendo elegir uno u otro según convenga. Su esquema (utilizado en los amperímetros), se muestra a continuación:
Veamos otro método con una evidente diferencia en la construcción. En esta ocasión según se aprecia en la figura 06, siguiente todas las resistencias se encuentran de algún modo sometidas al paso de la corriente, la cual dispone de dos caminos para su recorrido, pero como siempre una imagen mejor que …

La corriente I (en la entrada de 500µA) recorre dos por uno 460µA y 40µA por el otro, como y se hemos comentado. Para obtener más información sobre los cálculos específicos recomendamos visitar la documentación puentes de medida.
Las Leyes de Kirchoff
Las dos primeras leyes establecidas por Gustav R. Kirchhoff (1824-1887) son indispensables para los cálculos de circuitos, estas leyes son:
1. La suma de las corrientes que entran, en un nudo o punto de unión de un circuito es igual a la suma de las corrientes que salen de ese nudo. Si asignamos el signo más (+) a las corrientes que entran en la unión, y el signo menos (-) a las que salen de ella, entonces la ley establece que la suma algebraica de las corrientes en un punto de unión es cero:
(suma algebraica de I) Σ I = 0 (en la unión)2. Para todo conjunto de conductores que forman un circuito cerrado, se verifica que la suma de las caídas de tensión en las resistencias que constituyen la malla, es igual a la suma de las f.e.ms. intercaladas. Considerando un aumento de potencial como positivo (+) y una caída de potencial como negativo (-), la suma algebraica de las diferencias de potenciales (tensiones, voltajes) en una malla cerrada es cero:
(suma algebraica de E) Σ E – Σ I*R = 0 (suma algebraica de las caídas I*R, en la malla cerrada)
Como consecuencia de esto en la práctica para aplicar esta ley, supondremos una dirección arbitraria para la corriente en cada rama. Así, en principio, el extremo de la resistencia, por donde penetra la corriente, es positivo con respecto al otro extremo. Si la solución para la corriente que se resuelva, hace que queden invertidas las polaridades, es porque la supuesta dirección de la corriente en esa rama, es la opuesta.
Por ejemplo:
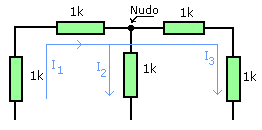
Las flechas representan la dirección del flujo de la corriente en el nudo. I1 entra a la unión, considerando que I2 e I3 salen. Si I1 fuera 20 A e I3 fuera 5 A, I2 tendría 15 A, según la ley de voltaje de I1=I2 + I3. La ley de Kirchoff para los voltajes es, la suma de voltajes alrededor de un circuito cerrado es igual a cero. Esto también puede expresarse como la suma de voltajes de un circuito cerrado es igual a la suma de voltajes de las fuentes de tensión:
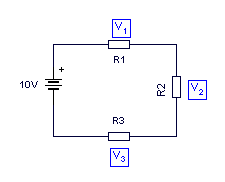
En la figura anterior, la suma de las caídas de voltaje en R1, R2 y R3 deben ser igual a 10V o sea, 10V =V1+ V2+ V3. Aquí un ejemplo:
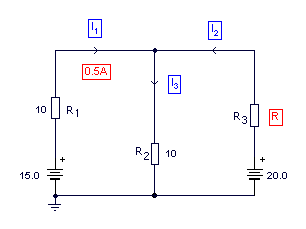
Las corrientes de I2 e I3 y la resistencia desconocida R3 centran todos los cálculos, usando la teoría básica de la corriente continua. La dirección del flujo de la corriente está indicado por las flechas.
- El voltaje en el lado izquierdo (la resistencia R1 de 10 Ω), está saliendo del terminal superior de la resistencia.
- La d. d. p. en esta resistencia R1 es de I1 * R o sea, 5 voltios. Esto está en oposición de los 15 voltios de la batería.
- Por la ley de kirchoff del voltaje, la d. d. p. por la resistencia R2 de 10 Ω es así 15-5 o sea, 10 voltios.
- Usando la ley Ohm, la corriente a través de la resistencia R2 10 Ω es entonces (V/R) 1 amperio.
- Usando la ley de Kirchoff de la corriente y ahora conociendo el I1 e I3, el I2 se encuentra como I3=I1+I2 por consiguiente el amperaje de I2= 0.5A.
- De nuevo, usando la ley de Kirchoff del voltaje, la d. d. p. para R3 puede calcularse como, 20 = I2*R3 +10. El voltaje por R3 (el I2*R3) es entonces 10 voltios. El valor de R3 es (V/I) o 10/0.5 o 20Ω.
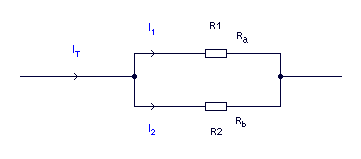
Los Divisores de corriente
La corriente que entra a un nodo sale dividida en dos partes, la corriente a través de una rama sale como se muestra debajo:
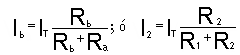

Los Divisores de tensión.